What Is A Travelling Salesman Problem (TSP)?

Table of Contents

The majority of field salespeople get up in the morning only having a general notion of what to do to make the best possible use of their workday. They want to reach multiple customers, as well as others along their journey that they are unaware of, however they might not follow a well-planned timetable. This weakness results in either retracing or getting out of time. The lack of sales route planning delays client meetings and missed opportunities.

Consider a salesperson who wants to go to several cities, but desires to cover as few miles as possible and come back to where they started. The Travelling Salesman Problem (TSP), a widely recognized problem, has remained the subject of research for more than a century. Finding the lowest possible weight Hamiltonian cycle that keeps both the travel expenses and the amount of distance travelled to a minimum is the salesman’s goal in the TSP.

What Is A Travelling Salesman Problem (TSP)?

The task of determining the shortest possible path or route for the salesman to travel provided a starting point, several cities (nodes), as well as a finishing point, is known as the “Travelling Salesman Problem” (TSP). This is a typical computational problem in fieldwork that could cause monetary damage and disrupt several field processes.

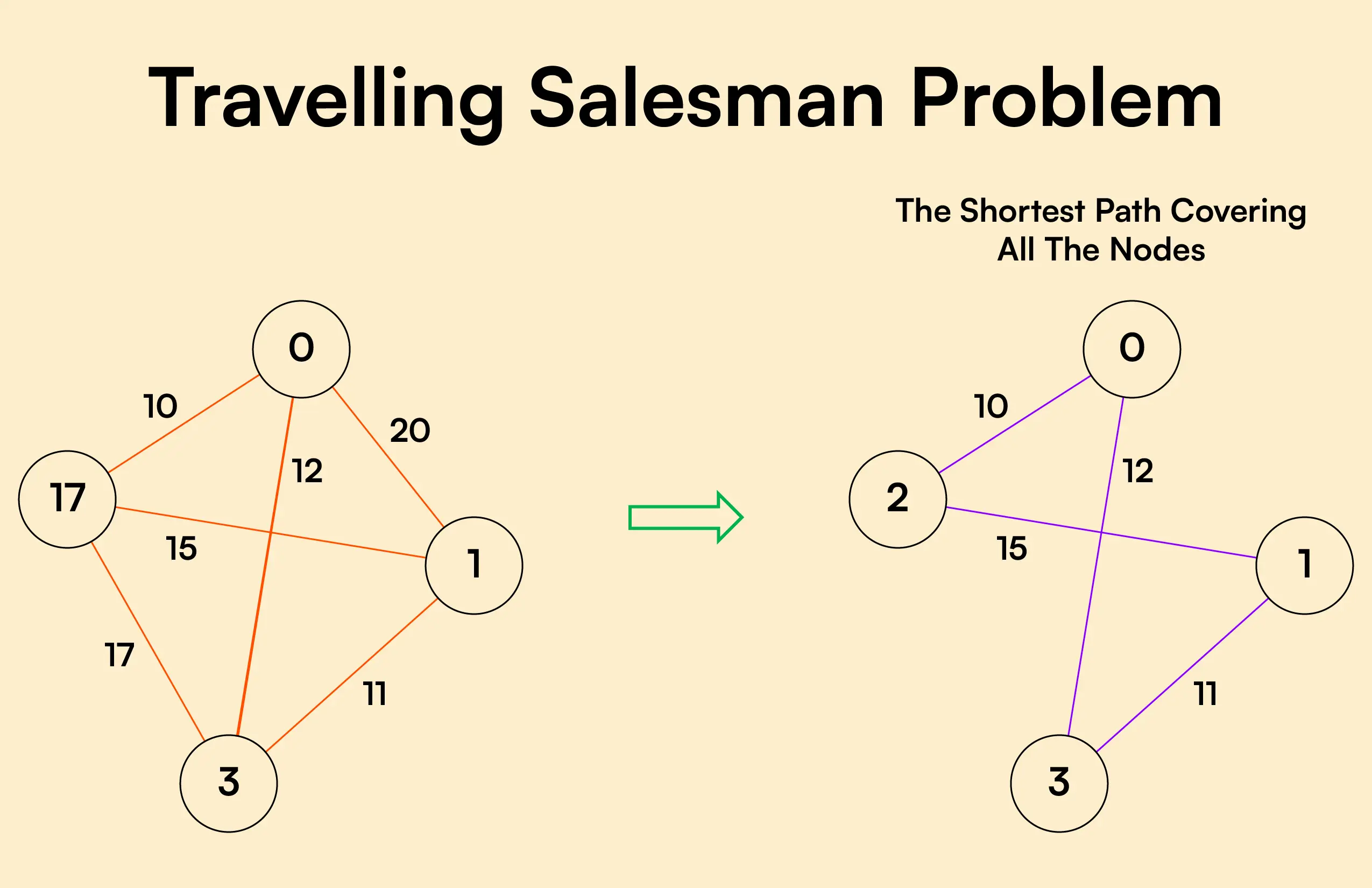
TSP occurs when there are several routes accessible but it is very difficult for you or the traveller to select the one with the lowest cost. By utilizing route optimization techniques to identify more profitable routes, field businesses can lower the release of greenhouse gases by travelling shorter distances.

What Is The History Of Travelling Salesman Problem?

The Travelling Salesman Problem, or TSP, has its roots at the beginning of the nineteenth century, but Merrill M. Flood was the first person to formalize it mathematically in 1930 while trying to figure out a school bus routing problem. The term “TSP” was first used in a 1949 RAND Corporation paper. It was then used by Hassler Whitney at Princeton under the title of the “48 states problem,” which meant the shortest path was examined for travelling all of the surrounding 48 United States.

The challenge of a salesperson travelling to several locations in the shortest amount of time, spending the smallest sum of money, and covering the shortest distance is only one aspect of TSP. The world is currently preparing for the fourth industrial revolution that will result in it. As advanced technology is included in the manufacturing process, TSP offers access to a broad range of functions. For example, a form of TSP could aid in the construction of an effective microprocessor. Analogously, by changing the location of colors, an asymmetric form of TSP can optimize the cost of setting up of a paint production unit.

Major Challenges Of Travelling Salesman Problem

When salespeople wake up, nearly every one of them considers how to best utilize their workday. They have a great deal of planned appointments as well as many impromptu ones with their clients. Being a salesperson is challenging since your daily routine will inevitably provide you with a number of obstacles. Some of the travelling salesmen challenges are:

First of all, salesmen are under constant time limitations as they complete numerous deliveries in a condensed amount of time each day. They must arrange their routes to maximize their potential in order to get around this.
The work schedules of salesmen are typically flexible. This defect commonly forces salespeople to go back and forth between their steps and take longer routes in order to get to client locations. This absence of planning for the journey leads to lost meetings and chances.
The salesperson nowadays faces road congestion, last-minute client demands, and tight delivery window timings along with the travel challenges that beset those before them.
Parallel to how salespeople modify their routes on the spot, the route algorithm needs to be adaptable and quick to sudden occurrences like traffic jams, automobile failures, and volume spikes. A TSP solution needs to be able to deal with complicated networks and huge databases with ease.
The number of routes grows dramatically in tandem with the number of destinations. The computing power of even the most advanced systems is surpassed by this hyperbolic development.

5 Most Reliable And Successful Solutions For The Travelling Salesman Problem

Since the first brute force technique was developed in the 1950s, TSP techniques have remained in use. Further refined methods like nearest neighbor algorithms and dynamic programming have been created since then. With the aid of all of these sophisticated algorithms, researchers and developers can now solve the TSP almost with the same speed and efficiency as they did before. One can solve the TSP in a much less amount of time by utilizing these algorithms.

The Brute Force Approach

In order to find the shortest distinct solution, the Brute Force method, sometimes referred to as the Naive Method, computes and contrasts each potential set of paths or routes. One has to first figure out the overall amount of routes, then sketch and list every feasible route in order to resolve the TSP employing the Brute-Force method. The best course of action is to determine each route’s distance and then select the one that is the shortest. This is rarely helpful outside of conceptual computing seminars and is only practical for small issues.

The Nearest Neighbour Approach

The most basic way to resolve the TSP is with this approach. This approach usually starts from the closest location, visiting all other locations, and then returning to the initial location. The following are the steps needed to solve the TSP employing the Nearest Neighbour approach:

Select an arbitrary location.
Find the closest unexplored location and get there.
The salesperson needs to go back to the starting point after visiting each location.

The Branch And Bound Approach

Determining the least cost for the rest of the routes that the beginning stages of methods such as the brute-force approach give is the focus of the branch and bound approach. Also known as Parallel TSP, this approach makes the assumption that we don’t wish to attempt every “possible” path. Even applying logic would likely help to simplify it.

We won’t, for instance, travel to the drop-off location that is the longest distance before we head back to the location that is closest to the warehouse. With the use of nodes and “costs” associated with each node, the approach calculates the likelihood that a particular option will result in a problem-solving solution.

Dynamic Programming

Dynamic programming is a method for handling intricate issues by breaking them down into smaller, easier-to-handle subproblems and addressing each one separately. It can find the shortest path that covers each city precisely once and avoids doing duplicate computations, which is why it is frequently used to solve the Travelling Salesman Problem. Because the method of dynamic programming can be utilized for solving issues of any size, it is more versatile than the brute force approach. Dynamic programming does have certain restrictions, though. It can be time-consuming and operationally costly because it requires the solution of a large number of smaller issues.

What Are Real-Time Travelling Salesman Problem Applications?

A widely recognized optimization problem with many practical applications across many industries is the travelling salesman problem (TSP). Every one of these practical uses exemplifies the TSP’s adaptability and the various challenges it has been used to tackle. Following are some of the TSP’s more noteworthy uses:

Vehicle Routing: Delivery and distribution route optimization is a common application of the TSP. Locations in this application correlate to delivery sites, and the salesperson is symbolized by a delivery vehicle. The idea is to determine the shortest path that makes precisely one stop at each destination before returning to the initial location. This issue is crucial in the world of delivery firms because it allows them to minimize fuel use, lower the number of vehicles needed, and guarantee the on-time distribution of products.

Logistics And Manufacturing: In the transportation and logistics sector, where businesses must optimize their supply routes to lower expenses and boost efficacy, the TSP is a prevalent issue. For instance, in order to save petrol and delivery time, a delivery service could have to determine the shortest path that stops at every one of its clients in a certain location.

The TSP is also applicable to production and manufacturing scheduling, as these fields require businesses to optimize their manufacturing processes to save expenses and boost productivity. For instance, in order to reduce downtime and increase production, a manufacturing facility may need to determine the quickest path to all of the machinery that requires maintenance.

Network Design And Optimization: In network architecture and optimization, the TSP is employed by businesses to optimize the flow of data, products, or services among a network of nodes. For instance, in order to reduce the loss of signal and enhance network efficiency, a telecommunications provider might need to determine the shortest path between its network nodes.

Circuit Design: The TSP is utilized in the area of electronics to create effective circuit schematics. In this case, the salesperson is the electrical signal that must pass via each city precisely once, and the cities are the circuit’s constituent parts. The objective is to determine the shortest path that minimizes the entire circuit’s resistance and impedance.

Robotics And Automation: The TSP also has applications in the fields of automation and robotics, where businesses must maximize machine or robot motion in order to cut expenses and boost productivity. For instance, in order to do different duties like choosing and arranging products or examining machinery, a robot might be required to determine the shortest route to take to every site in a plant.

How TSP Solves Last-Mile Delivery Problems?

The last step in a supply chain is the focus of the last-mile delivery issue. It entails moving cargo from a central point of transportation, like a terminal or warehouse, to the final destination.

Inadequate Route Planning
Delivery Windows
Traffic Congestions
High Travel/Fuel Costs
Late/Untimely Deliveries

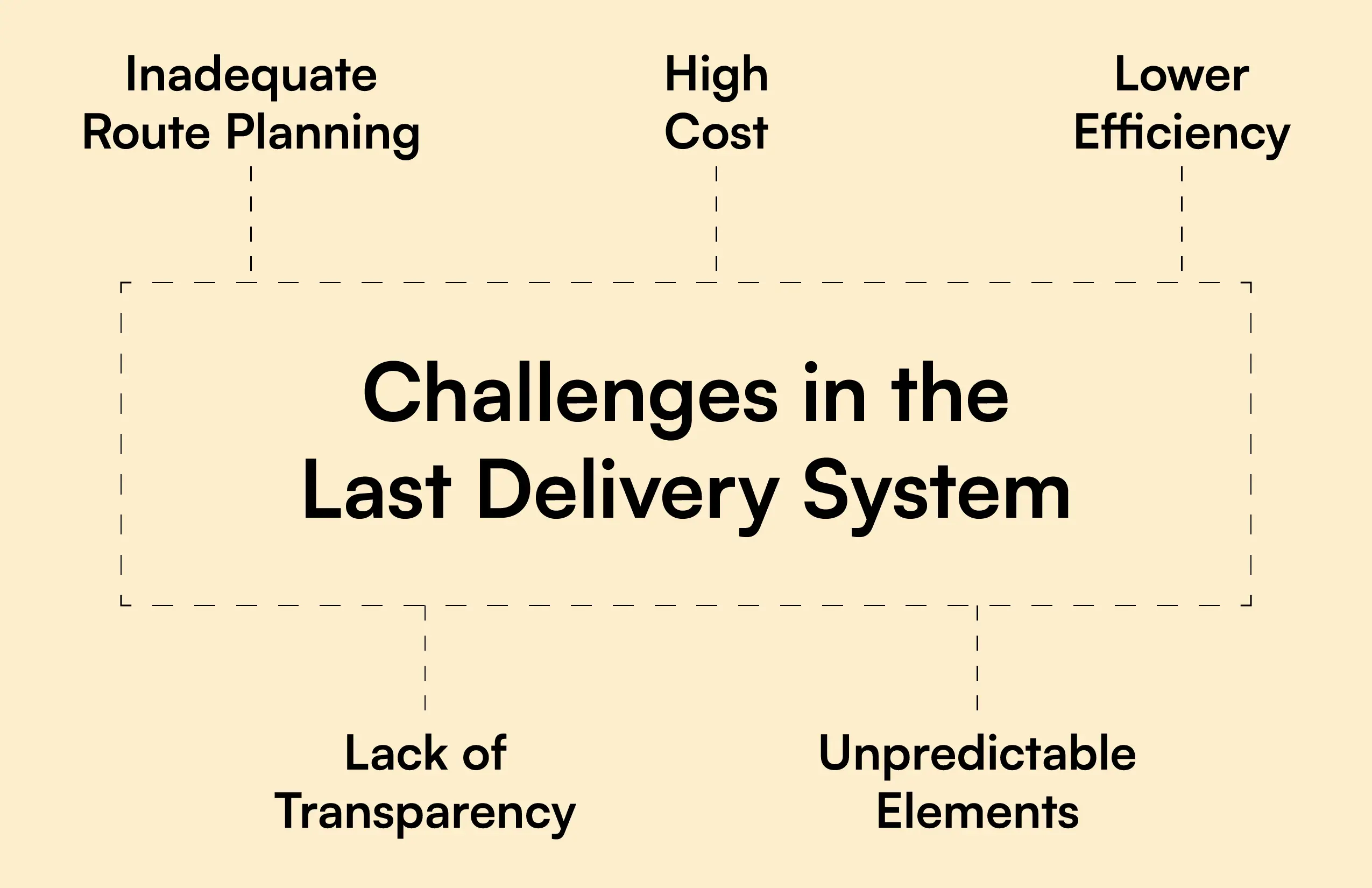
By streamlining routes for delivery, cutting down on stops, and minimizing the total kilometers travelled, TSP solutions are essential in tackling this problem. The Travelling Salesman Problem yields effective solutions that optimize and reduce last-mile delivery costs. These technologies assist delivery companies in identifying a series of courses or routes that minimize delivery expenses. A number of delivery destinations, warehouse locations, and delivery automobiles are all part of the delivery issue arena.

How AI Helps In Solving Travelling Salesman Problem (TSP)?

Artificial intelligence (AI) methods including neural networks, genetic algorithms, and ant colony optimization were all used to solve the TSP effectively. Supply chain management and logistics have benefited greatly from AI. This involves enhancing transportation routes or reducing the amount of miles driven when delivering products. The use of artificial intelligence assists business operational leaders in creating and allocating the best possible sales plans for their employees. It provides the best possible meeting plans by accounting for factors such as proximity, automobile capacity, client time window, salespeople’s abilities, driver skills, and many more.

We can anticipate significantly more advanced applications in TSP solutions given the swift development in AI. This might entail the creation of novel artificial intelligence methods that can deal with bigger and more complicated problems or the application of quantum algorithms for faster resolution. The development of AI has revolutionized the way we approach and deal with these issues, increasing productivity and effectiveness across a range of businesses. We do not doubt that AI will play a substantially greater role in resolving TSP and related issues as the technology develops.

Conclusion

The Travelling Salesman Problem is a complex statistical puzzle that simulates the daily activities of a salesperson. It describes the endeavors of a door-to-door salesperson who is attempting to determine the most efficient and/or fastest manner to complete all of the locations on their list of visits in a specific amount of time (often a workday). Initially, it used to be a salesperson’s issue, but far more people deal with it nowadays.

Field workers can learn about optimization concepts and use them when dealing with a range of real-world issues through exploring the TSP. Even though the TSP is still a difficult issue, advances in computer technology and algorithms have made it easier to get to and solve. In the end, solving the TSP along with other challenging optimization issues can enhance both our personal life and the world that we dwell in.